Lisämateriaaleja lukion fysiikkaan

Tämä luku liittyy läheisesti lukion fysiikan kurssiin/moduuliin FY05 Jaksollinen liike ja aallot (uusi ja vanha lops). Tasaisen ympyräliikkeen ja normaalikiihtyvyyden käsittelyn yhteydessä voi tätä materiaalia hyödyntämällä käsitellä esimerkiksi kiihtyvään ympyräliikkeessen liittyviä käsitteitä.

Tämän luvun osiot alkavat aiheeseen liittyvällä opetusvideolla, jonka pohjalta vastataan muutamaan kysymykseen. Tarkoituksena on oppia olennaiset asiat pyörimisliikkeestä ja vierimisestä. Alussa esitellään haastava ongelma, jonka ratkaisemista varten kerrytetään esitietoja. Ongelmaan palataan materiaalin lopussa ja ongelma ratkaistaan tukikysymysten avulla.

Osioissa 1-6 käsitellään lukion fysiikan näkökulmasta jäykän kappaleen dynamiikkaan liittyviä asioita. Luvussa 1 motivoidaan aiheeseen ja esitellään aiheeseen liittyviä käsitteitä. Osiot 2 ja 3 käsittelevät yleistä pyörimisliikettä. Osio 4 esittelee pyörimisliikkeen perusyhtälön ja hitausmomentin, osio 5 rotaatioenergian ja sen säilymislain ja osio 6 pyörimismäärän ja sen säilymisen.

Osiossa 7 syvennetään aiempien lukujen käsitteitä matemaattisemmalla lähestymistavalla. Osion 7 esitietoina olisi hyvä olla perustiedot vektoreista, derivaatasta ja integraalista (polynomien integrointi). Osiota 7 ei tarvita alussa esitellyn tehtävän ratkaisemisessa, mutta tietojen syventämisestä on hyötyä.

Osiossa 8 ratkaistaan tuetusti alussa esitelty ongelma. Ongelma on ollut osatehtävänä vuoden 2014 kansainvälisissä fysiikkaolympialaisissa (ipho). Materiaalin lopussa on vastaukset tehtäviin.

Osioihin 2-6 liittyy 1-2 n. 10 minuuttia kestävää videota ja 2-4 tehtävää. Tehtävät ovat käsitteellisiä ja yksinkertaisia laskuja vaativia tehtäviä. Näiden lukujen käsittelyyn on hyvä varata 20-45 minuuttia. Osio 7 on jaettu kolmeen alalukuun, joihin liittyy jälleen 1-2 videota ja pari tehtävää. Nämä videot ovat sisällöltään aiempia haastavia. Yhden osion 7 alaosion käsittelyyn on syytä varata 30-45 minuuttia.

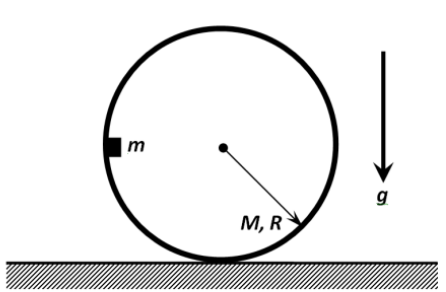
Tarkoituksenamme on oppia analysoimaan kuvassa näkyvää systeemiä. Pieni \(m\)-massainen kiekko on asetettu onton ohuen sylinterin sisäpinnalle. Sylinterin massa on \(M\) ja säde \(R\text{.}\) Aluksi sylinteri lepää vaakasuoran tason päällä, ja kiekko on korkeudella \(R\) tasosta. Tehtävänämme on löytää kiekon sylinteriin aiheuttama tukivoima \(F\text{,}\) kun kiekko saavuttaa ratansa matalimman kohdan. Oletamme, että kiekon ja sylinterin välillä ei ole kitkaa ja että sylinteri vierii liukumatta. Putoamiskiihtyvyys on \(g\text{.}\)

Tehtävän ratkaisemiseksi tarvitsemme esitietoja jäykän kappaleen pyörimisliikkeestä ja vierimisestä. Tututstumme käsitteisiin kulmakiihtyvyys, normaalikiihtyvyys, vierimisehto, rotaatioenergia, hitausmomentti ja pyörimismäärä. Tutustumme siihen, miten mekaaninen energia säilyy pyörimisliikkeessä ja miten kappaleen muoto vaikuttaa sen vierimiseen.

(Tehtävä on osatehtävä vuoden 2014 kansainvälisistä fysiikkaolympialaisista, ks. IPhO.)