Alaluku 6.1 Vektorit
Fyysikoilla on useita tapoja merkitä vektoreita erilaisten mieltymysten ja soveltuvuuksien mukaan. Kaikki nämä merkinnät ovat yhtäläisiä. Joskus on tarpeen korostaa vektorin komponentteja ja joskus täytyy erottaa vektorisuureet skalaareista.
Tässä materiaalissa käytetään kirjaimen yllä olevaa nuolta merkitsemään vektoreita: \(\vec{v}\text{.}\)
Yksikkövektoreita merkitään kirjaimen päällä olevalla hatulla. Karteesisten akselien (\(x\text{,}\)\(y\) ja \(z\)-akselien) suuntaisia yksikkövektoreita merkitään yleensä \(\hat{i}, \hat{j}, \hat{k} \) ja yleistä johonkin muuhun suuntaan osoittavaa yksikkövektoria esimerkiksi \(\hat{r}\text{.}\)
Joskus käytetään toista tapaa merkitä akselien suuntaisia yksikkövektoreita
Vektorin voi esittää sen komponenttien ja yksikkövektoreiden avulla aiempia merkintätapoja käyttämällä
Vektorisuure voi riippua ajasta tai jostain muusta suureesta, jolloin se on funktio
Vektorin pituutta merkitään usein samalla kirjaimella kuin vektoria
mutta sekaannusten välttämiseksi on syytä suosia merkintää \(|\vec{r}|\text{.}\)
Erilaisia fysiikassa esiintyviä vektorisuureita ovat esimerkiksi: nopeus, kiihtyvyys, liikemäärä, voima, pyörimismäärä, sähkökenttä, magneettikenttä ja dipolimomentti.
Fysiikassa esiintyy myös funktioita, jotka riippuvat useasta muuttujasta. Katso video Kahden muuttujan funktio. Fysikaalinen esimerkki tällaisesta funktiosta voi olla vaikkapa paikasta riippuva sähkökenttä
Huomaa, että monen muuttujan funktion voi käsittää funktiona, jonka muuttujana on vektori.
Koska nopeus on vektori, myös liikemäärä on silloin vektori
Newtonin II:n lain voi kirjoittaa vektorien ja derivaattojen avulla eri muodoissa
Sähkövaraukset kohdistavat toisiinsa Coulombin voiman
jossa \(\vec{r}_1\) ja \(\vec{r}_2\) ovat varausten paikkavektorit.
Pistemäinen varaus luo sähkökentän
jossa \(\vec{r}\) on paikkavektori tutkittavasta pisteestä varaukseen.
Alaluku 6.1.1 Komponentteihin jakaminen
Monessa fysiikan ongelmassa vektorin komponentit ovat tärkeitä ja helpottavat tutkittavan ilmiön dynamiikan tarkastelua. Montaa tilannetta voi tarkastella \(xy\) -koordinaatistossa siten, että \(\theta\) on kiertokulma \(x\)-akseliin nähden. Tällöin vektorin \(\vec{r}\) komponentit ovat
Harjoitustehtävät Harjoitustehtävät
1.
Mikä on sähkökentän voimakkuus ja suunta alla olevan kuvan merkityssä pisteessä?
Merkitään ylempää varausta \(q_1\text{:}\)llä ja alempaa varausta \(q_2\text{:}\)lla. Molemmat varaukset ovat positiivisia, joten sähkökenttä pisteessä \(P\) osoittaa poispäin varauksista. Kiinnitetään koordinaatisto siten, että varaukset sijaitsevat y-akselilla ja origo on pisteiden puolessavälissä.
\(q_1\text{:}\)n aiheuttama sähkökenttä on
ja suunta on \ang{45} x-akselista alavasemmalle. Akseleiden suuntaisten yksikkövektoreiden \(\hat{i}\) ja \(\hat{j}\) avulla
Vastaavasti varauksen \(q_2\) sähkökentäksi saadaan
2.
Kirjoita heittoliikkeessä olevan kappaleen nopeuden \(x\)- ja \(y\)-komponentit ajan funktiona, kun alkunopeus \(v\) ja heittokulma \(\theta\) tunnetaan. Voit olettaa ilmanvastuksen pieneksi.
Kun ilmanvastus oletetaan pieneksi, heittoliikkeessä olevaan kappaleeseen vaikuttaa ainoastaan painovoima suoraan alaspäin. Tällä voimalla ei ole x-suuntaista komponenttia. Siispä nopeuden x-komponentti ei muutu ja se saadaan trigonometrialla
Pystysuuntainen nopeus muuttuu ajassa kiihtyvyydellä \(-g\text{.}\) Alkunopeus saadaan jälleen trigonometrialla
Tasaisesti muuttuvalle nopeudelle \(v= v_0 + at\text{,}\) joten heittoliikkeen y-suuntainen komponentti on
3.
Kaksi 5,0 g:n pistevarausta 1,0 m pitkissä naruissa hylkivät toisiaan, kun varausten suuruudet on +100 nC, kuten alla olevassa kuvassa. Mikä on \(\theta\text{?}\) Voit käyttää pienillä kulmilla hyvin toimivaa approksimaatiota \(\tan\theta \approx \sin\theta\text{.}\)
Kannattaa piirtää varausten vapaakappalekuvat
Varaukset ovat tasapainossa ja lanka muodostaa kulman \(\theta\) pystysuunnasta. Varauksiin vaikuttaa sähköinen voima, painovoima ja langan jännitysvoima.
Tasapainossa Newtonin ensimmäinen lain mukaan kappaleeseen vaikuttava kokonaisvoima on nolla, eli \(\vec{F}_\mathrm{kok} = \vec{T} + \vec{F}_\mathrm{G} + \vec{F}_\mathrm{e} = \vec{0} \text{.}\) Komponenteittain
Jaetaan vasemmanpuoleinen yhtälö oikeanpuoleisella, jolloin saadaan
Pienille kulmille \(\tan\theta \approx \sin\theta \text{.}\) Tällä approksimaatiolla saadaan \(\sin\theta=0,0771\text{,}\) joten \(\theta=\ang{4,4}\text{.}\)
4.
Alla olevassa kuvassa on kolme toisiinsa sidottua köyttä. Yksi ystäväsi vetää köyttä 3,0 N:n voimalla ja toinen 5,0 N:n voimalla. Millä voimalla ja mihin suuntaan sinun tulee vetää köyttä, jotta solmu pysyisi paikallaan?
Käsitellään köydessä olevaa solmua staattisessa tasapainossa olevana hiukkasena.
Kirjoitetaan vektorit \(\vec{F}_1\) ja \(\vec{F}_2\) komponenttimuodossa. Nyt \(\vec{F}_1=3\hat{i}\) ja \(\vec{F}_2=-5\sin(\ang{30})\hat{i} + 5\cos(\ang{30})\hat{j} \text{.}\) Tasapainossa voimien summan täytyy olla 0, eli \(\vec{F}_1 + \vec{F}_2 + \vec{F}_3 = \vec{0}\text{.}\) Voimme ratkaista tuntemattoman voiman \(\vec{F}_3 = -\vec{F}_1 - \vec{F}_2 = -0,5\hat{i} - 4,33\hat{j}.\) Voiman 3 suuruus on \(F_3 = \sqrt{(-0,50)^2+(-4,33)^2} = 4,4\text{.}\) Kulma \(\theta = \tan^{-1}(4,33/0,50) = \ang{83}\) negatiivisesta x-akselista alaspäin.
5.
Mikä on sähkökentän suunta ja voimakkuus merkityssä pisteessä?
Lasketaan eri varausten aiheuttamat sähkökentät ja summataan ne yhteen. Merkitään varauksia \(q_1=\SI{5,0}{\nano\coulomb}, q_2=\SI{10}{\nano\coulomb}, q_3=\SI{-5,0}{\nano\coulomb}\text{.}\)
Varauksen \(q_1\) aiheuttama kenttä on
Varauksen \(q_2\) aiheuttama kenttä on
Varauksen \(q_3\) aiheuttaman kentän suuruus on
\(\vec{E}_3\) osoittaa kohti \(q_3\text{:}\)a ja muodostaa kulman \(\theta=\tan^{-1}(4/2)=\ang{63,43}\) x-akseliin nähden. Siispä
Näiden vektorien summa on
Sähkökentän voimakkuus on
ja vektorin muodostama kulma x-akselista on
Alaluku 6.1.2 Pistetulo
Jos tarvitset muistin virkistystä vektoreiden pistetulosta, voit katsoa videon Pistetulo.
Harjoitustehtävät Harjoitustehtävät
Vakiovoiman tekemä työ on yleisesti
kun voima ja liikkeen suunta eivät ole samansuuntaiset. Kun ne ovat samansuuntaiset, pistetulo muuttuu kertolaskuksi ja saadaan tuttu \(W=Fs\text{,}\) eli työ on matka kertaa voima.
1.
Kuinka paljon voima \(\vec{F} = (-3,0\hat{i} + 6,0\hat{j})\si{\newton}\) tekee työtä hiukkaseen, joka liikkuu siirtymän
(a)
\(\Delta \vec{r} = 2,0\hat{i}\;\si{\meter}\)
(b)
\(\Delta \vec{r} = 2,0\hat{j}\;\si{\meter}\)
2.
Kahta köyttä käytetään pianon laskemiseksi toisesta kerroksesta maahan. Pianon massa on 355 kg ja siirron korkeus on 5,00 m. Kuinka paljon eri voimat tekevät työtä?
Lasketaan voimien tekemät työt pistetulolla \(W=\vec{F}\cdot\Delta\vec{r}\text{.}\) Siirtymä on \(\Delta \vec{r}=-5,00\hat{j}\text{.}\) Painovoimalle
Jännitysvoimalle 1
Jännitysvoimalle 2
3.
Hiihtäjä, jonka massa on 60 kg ja nopeus on 2,0 m/s, saapuu mäkeen, jonka pituus on 50 m ja kaltevuuskulma \(\ang{10}\text{.}\) Mikä on hiihtäjän nopeus mäen alla, jos oletetaan, että hiihtäjä liukuu kitkatta mäkeä alas?
Tarkastellaan hiihtäjää pistemäisenä kappaleena. Piirretään tilanteesta kuva
Kineettisen energian muutos \(\Delta K\) on yhtäsuuri kuin painovoiman hiihtäjään tekemä työ. Lasketaan työ pistetulon avulla ja ratkaistaan kineettisten energioiden erotuksesta \(v_1\text{.}\)
Työksi saadaan
Ratkaistaan nopeus kineettisen energian muutoksesta
Teho on yksinkertaisessa tapauksessa \(P=W/t\text{,}\) eli tehty työ jaettuna työhön käytetyllä ajalla. Toisin sanoen teho kertoo kuinka nopeasti työtä tehdään aikayksikössä. Tämän voi ilmaista derivaatan avulla \(P = \dee W/ \dee t\text{.}\) Työn määritelmästä saadaan pienen matkan \(\dee \vec{r}\) yli tehty työ
jolloin tehoksi saadaan
Eli voiman hiukkaseen kohdistama teho on voiman ja hiukkasen nopeuden pistetulo.
4.
Tehtaassa siirretään 300 kg konetta moottorin avulla. Mikä moottorin tehon on oltava, jotta kone liikkuu 5 m/s? Koneen ja lattian välinen kitkakerroin on \(\mu=0,60\text{.}\)
Moottori kohdistaa kaapelin välityksellä koneeseen jännitysvoiman \(\vec{T}\text{.}\) Tämä voima tekee koneeseen työtä teholla \(P=Tv\text{.}\) Kone on tasapainossa, koska se liikkuu tasaisella nopeudella, joten kaapelin jännitysvoima on yhtäsuuri kuin kitkan aiheuttama voima
Moottorin tehoksi saadaan
5.
1500 kg auto, jonka etuprofiilin leveys on 1,6 m ja korkeus on 1,4 m. Auton ilmanvastuskerroin on 0,50 ja renkaiden ja tien välinen vierimiskitkakerroin on 0,02. Mikä moottorin tehon on oltava, jotta auto voi ylläpitää nopeutta \(\SI{30}{\meter/\second} = \SI{108}{\kilo\meter/\hour}\text{.}\) Oleta, että auton moottorin tehosta 25% kuluu muuhun kuin renkaiden pyörittämiseen. Vierimiskitkalle voit käyttää \(f_\mu = \mu m g\) ja ilmanvastukselle \(F_{\mathrm{D}} = \frac{1}{2} C \rho A v^2\text{,}\) jossa \(C\) on kappaleen muodosta tuleva kerroin, \(\rho\) on väliaineen tiheys, \(A\) on kappaleen poikkileikkauksen pinta-ala ja \(v\) on kappaleen vauhti.
Tasaisella nopeudella liikkuvaan autoon kohdistuva kokonaisvoima on nolla. Liikettä vastustavat renkaiden vierimiskitka ja ilmanvastus. Autoa eteenpäin työntävä voima \(\vec{F}\) on yhtäsuuri kuin vastusvoimien summa
jossa \(\vec{D}\) on ilmanvastus. Annetuilla tiedoilla
jossa \(A\) on auton poikkileikkauksen ala ja \(\rho=\SI{1,2}{\kilogram/\meter\cubed}\) ilman tiheys. Teho, joka tarvitaan auton nopeuden pitämiseksi 30 m/s, on
Auton vetävien renkaiden täytyy siis tuottaa tämä teho vastusvoimia vastaan. Moottorin tuottaman tehon täytyy olla suurempi, koska osa moottorin tehosta kuluu auton toimintaan ja osa menee hukkaan. Jos 25% tehosta menetetään, niin autoa liikuttavasta tehosta saadaan moottorin tuottama teho
Alaluku 6.1.3 Ristitulo
Katso videot Determinantit (Matikkamatskut) ja Ristitulo (Matikkamatskut).
Fysikaalisissa tilanteissa ristitulon voi usein määrittää laskematta käyttämällä oikean käden sääntöä (kuva 1). Oikean käden etusormi osoittaa ensimmäisen vektorin suuntaan, kohtisuoraan etusormen kanssa oleva keskisormi osoittaa toisen vektorin suuntaan ja peukalo osoittaa ristitulon tuloksen suuntaan. Yhtäläisesti oikean käden säännön voi määritellä siten, että peukalo ja etusormi osoittavat keskenään kerrottavien vektoreiden suunnat ja keskisormi osoittaa saadun vektorin suunnan.
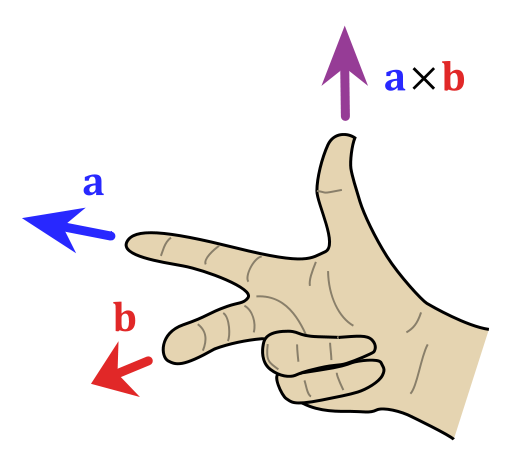
Harjoitustehtävät Harjoitustehtävät
1.
Määritä yksikkövektoreiden väliset ristitulot
Pistemäinen liikkuva varattu hiukkanen luo magneettikentän
2.
Alla olevan kuvan elektroni liikkuu oikealle. Mihin suuntaan elektronin luoma magneettikenttä osoittaa merkityssä pisteessä?
Huomaa, että varauksen merkki muuttaa ristitulosta saatavan vektorin suunnan. Magneettikenttä osoittaa siten sivusta ulospäin.
Magneettikentässä liikkuvaan hiukkaseen kohdistuva voima riippuu sen nopeudesta
3.
Pitkässä johtimessa kulkee 10 A virta vasemmalta oikealle. 1,0 cm:n etäisyydellä johtimen yläpuolella liikkuu elektroni oikealle nopeudella 1,0e7 m/s. Mikä on magneettikentän elektroniin kohdistaman voiman suunta ja suuruus?
Varaus on negatiivinen, joten voiman suunta on päinvastainen vektoriin \(\vec{v}\times\vec{B}\) nähden. Oikean käden säännöstä saadaan, että \(\vec{v}\times\vec{B}\) osoittaa alaspäin, joten voiman \(\vec{F}\) suunta on ylös. Voiman suuruus on \(F=|q|vB\) ja magneettikenttä on pitkän suoran johtimen kenttä
joten voiman suuruus on
ja suunta ylös, kuten todettiin.
Lorentzin voima kuvaa varattuun hiukkaseen kohdistuvaa voimaa sähkö- ja magneettikentässä.
Kun nopeus on kohtisuorassa magneettikenttää vasten ja sähkökenttää ei ole, hiukkanen on ympyräradalla. Jos ristitulon kirjoittaa auki determinantin avulla, voi nähdä, miten voima saa magneettikentän suuntaista komponenttia, kun nopeus ei ole kohtisuorassa magneettikentän kanssa. Tällöin hiukkanen päätyy ruuviviivaradalle.
Voima ei aina kohdistu kohtisuoraan voiman vartta kohden, joten yleisempi muoto vääntömomentille on tarpeen. Vääntömomentissa
\(r\) on etäisyys pisteestä, jonka suhteen kappale pyörii pisteeseen, johon voima vaikuttaa. Huomaa, että kulma \(\phi\) on voiman varren ja voimavektorin välinen kulma.
4.
Käytät 20 cm pitkää jakoavainta mutterin vääntämiseen. Jakoavaimen varsi muodostaa \(\ang{30}\) kulman vaakatasoon nähden ja kohdistat jakoavaimen päähän 100 N voiman. Kuinka suuri vääntömomentti kohdistuu mutteriin?
Piirretään havainnollistava kuva.
Lasketaan vääntömomentti ristitulon trigonometrisella määritelmällä, huomaa \(\phi\text{:}\)n merkki
Hiukkasen pyörimismäärä jonkin pisteen suhteen saadaan ristitulolla
5.
Mihin suuntaan pyörimismäärävektori osoittaa, kun hiukkanen on ympyräradalla \(xy\)-tasossa?
Jos hiukkanen liikkuu vastapäivään, pyörimismäärävektori osoittaa positiivisen z-akselin suuntaan. Jos liike on myötäpäivään, vektorin suunta on negatiivisen z-akselin suuntaan.
Magneettinen dipolimomentti määritellään magneettikentän dipoliin aiheuttaman vääntömomentin avulla \(\vec{\tau} = \ristitulo{m}{B}\text{.}\)