LuFy Palataan alun systeemiin

Siirry pääasiaan

Alaluku 1.8 Palataan alun systeemiin

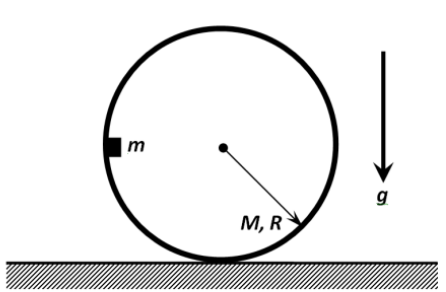
Pieni \(m\)-massainen kiekko on asetettu onton ohuen sylinterin sisäpinnalle. Sylinterin massa on \(M\) ja säde \(R\text{.}\) Aluksi sylinteri lepää vaakasuoran tason päällä, ja kiekko on korkeudella \(R\) tasosta. Tehtävänämme on löytää kiekon sylinteriin aiheuttama tukivoima \(F\text{,}\) kun kiekko saavuttaa ratansa matalimman kohdan. Oletamme, että kiekon ja sylinterin välillä ei ole kitkaa ja että sylinteri vierii liukumatta. Putoamiskiihtyvyys on \(g\text{.}\)

(for accessibility)

Tarkastellaan tätä tehtävää paloittelemalla se osatehtäviin. Pohditaan kuitenkin aluksi sitä, miten tällaista haastavaa tehtävää voi lähteä tutkimaan ja analysoimaan. Muutamaa vaihtoehtoa kannattaa pysähtyä hetkeksi miettimään: Mikä on se suure, jonka tietämisestä olisi tehtävän ratkaisun kannalta eniten hyötyä? Voiko tilannetta yksinkertaistaa ja ratkaista helpomman ongelman? Voiko samoja periaatteita hyödyntää monimutkaisemman ongelman ratkaisemisessa? Tällaiset kysymykset ovat yleisestikin hyödyllisiä matematiikan ja fysiikan ongelmien ratkaisemisessa. Erilaisia kilpailu- ja oppikirjatehtäviä ratkoessa on myös hyvä muistaa, että yleensä tehtäviin on olemassa analyyttinen ratkaisu tai jos ei ole, se kerrotaan tehtävänannossa.

Harjoitustehtävät Harjoitustehtävät

Piirrä tilanteesta ensin havainnollistava kuva, josta ilmenee ainakin kiekkoon ja sylinteriin vaikuttavat voimat, kun kiekko on liukumassa ala-asentoon ja kun kiekko on ala-asennossa.

Pohdi seuraavia kysymyksiä ennen kuin etenet:

1.

Mitkä suureet sinun tarvitsee tietää, jotta saat selville kysytyn voiman \(F\text{?}\)

Esimerkiksi kiekon ratanopeus sylinterin keskipisteen suhteen, sylinterin keskipisteen nopeus.

2.

Mitkä asiat sinun täytyy tietää, jotta voit saada nämä edelliset suureet selville?

Esim. sylinterin kulmakiihtyvyys ja kulmanopeus.

3.

Mikä tästä ongelmasta tekee haastavan? Eli minkä tehtävän piirteen voi yksinkertaistaa ja ratkaista helpomman ongelman?

Sylinterin liikkuminen on koko tehtävän juju.

4.

Miten ongelma ratkeaisi tällä yksinkertaistuksella?

Ilman sylinterin liikettä tehtävän voi ratkaista kirjoittamalla kiekolle mekaanisen energian säilymisen ja ratkaisemalla sen avulla kiekon ratanopeuden.

Seuraavaksi pohditaan sitä, miltä kysymyksen lopputilanne näyttää. Analysoidaan siis tilannetta, jossa kiekko on jo ala-asennossa.

5.

Mihin suuntaan kiekon nopeus ja kiihtyvyys osoittavat?

Kiekon nopeus on x-akselin suuntainen ja kiihtyvyys y-akselin suuntainen (suoraan sylinterin keskipistettä kohti).

6.

Mihin suuntaan sylinterin keskipisteen nopeus ja kiihtyvyys osoittavat?

Sylinterin keskipisteen nopeus on x-akselin suuntainen ja kiihtyvyys on hetkellisesti 0.

Yksinkertaisempi ongelma olisi sellainen, jossa sylinteri on kiinnitetty paikalleen. Tässä tilanteessa kiekon nopeus ala-asennossa saadaan suoraviivaisesti energian säilymislailla. Tämä ongelma kannattaa ratkaista ennen etenemistä. Seuraavaksi tutkimme sylinterin liikettä.

7.

Kirjoita sylinterin liikeyhtälö käyttämällä Newtonin toista lakia.

Mieti sylinterin keskipisteen liikettä. Sylinterin keskipiste liikkuu x-akselin suuntaisesti, joten voit tutkia x-suuntaan vaikuttavia voimia.

\begin{equation*} Ma_s = N \sin \theta - F_{fr} \end{equation*}

8.

Kirjoita sylinterin kulmakiihtyvyys sylinterin keskipisteen kiihtyvyyden avulla.

Vierimisehto

\begin{equation*} \alpha = a_s / R \end{equation*}

9.

Mikä on sylinteriin kohdistuvan kitkavoiman suuruus?

Sylinterin ja tason välinen kitka aiheuttaa vääntömomentin.

\begin{equation*} \tau = I \alpha = F_{fr}R \iff F_{fr} = MR^2 \frac{a_s}{R} \frac{1}{R} = M a_s \end{equation*}

Seuraavaksi tutkitaan sitä, miten kiekon ja sylinterin kiihtyvyydet liittyvät toisiinsa.

10.

Kirjoita kiekon \(x\)- ja \(y\)-suuntaiset kiihtyvyydet kiekon ja sylinterin välisen tukivoiman avulla.

\begin{equation*} a_x = N \sin \theta, \quad a_y = N \cos \theta \end{equation*}

11.

Ratkaise aiemmin tutkimasi sylinterin kiihtyvyys kiekon ja sylinterin välisen tukivoiman suhteen.

\begin{equation*} M a_s = N \sin \theta - F_{fr} = N \sin \theta - M a_s \iff 2 M a_s = N \sin \theta \end{equation*}

12.

Saatko nyt kirjoitettua sylinterin keskipisteen x-suuntaisen kiihtyvyyden kiekon x-suuntaisen kiihtyvyyden avulla?

\begin{equation*} 2 M a_s = m a_x \end{equation*}

13.

Laske kiihtyvyyksistä sylinterin ja kiekon x-suuntaiset nopeudet toistensa suhteen.

Integroi saamasi yhtälö 0:sta \(t\text{:}\)hen.

\begin{equation*} 2 M v = m u \end{equation*}

Tutkitaan nyt, saammeko kirjoitettua kiekon ja sylinterin x-suuntaiset nopeudet käyttämällä ainoastaan tehtävässä annettuja tietoja.

14.

Mitä fysiikan periaatetta voit nyt hyödyntää?

Säilymislaki

Mekaanisen energian säilyminen. \(E_{p,kiekko} = E_{k,kiekko} + E_{k,sylinteri} + E_{rot,sylinteri}\text{,}\) eli

\begin{equation*} mgR = \frac{1}{2} mu^2 + \frac{1}{2} mv^2 + \frac{1}{2} I \omega^2 \end{equation*}

15.

Sijoita saamaasi yhtälöön sylinterin kulmanopeus.

Vierimisehto

\(\omega = \frac{v}{R}\)

16.

Ratkaise yhtälöparista nopeudet.

Kysymyksen 12 ja 15 yhtälöt.

\begin{equation*} u = 2 \sqrt{\frac{MgR}{2M+m}}, \quad v = \frac{m}{M} \sqrt{\frac{MgR}{2M+m}} \end{equation*}

Olemme jo hyvin lähellä ratkaisua. Palautetaan tässä vaiheessa mieleen se, mitä alunperin kysyttiin. Kysymys kuului, mikä on kiekon sylinteriin aiheuttama tukivoima, kun kiekko on ala-asennossa. Jos pohdit aiemmin tämän hetkellisen tilanteen nopeuksia ja kiihtyvyyksiä, totesit että kiekon nopeus on x-akselin suuntainen ja kiihtyvyys suoraan ylöspäin eli sylinterin keskipistettä kohti. Kiekko on siis sylinterin keskipisteen suhteen hetkellisesti ympyräliikkeessä. Sylinteriin taas ei kohdistu tällä hetkellä kokonaisvoimaa x-akselin suuntaan, joten sylinteri on hetkellisesti tähän suuntaan tasaisessa liikkeessä. Näillä tiedoilla voimme laskea kiekon ratanopeuden suhteessa sylinterin keskipisteeseen ja laskea tutulla tavalla ympyräliikkeessä olevan kappaleen normaalikiihtyvyydestä aiheutuvan voiman.

17.

Mikä on kiekon nopeus suhteessa sylinterin keskipisteeseen?

Galilein muunnos sylinterin keskipisteen mukana liikkuvaan koordinaatistoon.

\begin{equation*} v_{rel} = u + v \end{equation*}

18.

Mikä on kiekon normaalikiihtyvyys tässä koordinaatistossa?

\begin{equation*} a_{rel} = v_{rel}^2 / R \end{equation*}

19.

Mikä on kiekon kiihtyvyys laboratoriokoordinaatistossa (aluksi valitsemassasi koordinaatistossa?)

Mitä seuraa siitä, että sylinterin kiihtyvyys on hetkellisesti 0?

\begin{equation*} a = a_{rel}\text{,} \end{equation*}

miksi?

20.

Laske kiekon sylinteriin kohdistama tukivoima.

\(F - mg = v_{rel}^2 / R\text{,}\) johon sijoittamalla \(v_{rel}\) saamme lopulta

\begin{equation*} F = 3mg \left( 1 + \frac{m}{3M} \right) \end{equation*}